PayPayの100億円あげちゃうキャンペーンは利用されましたか。
すぐにキャンペーン終了となってしまい、参加する間もなく終わってしまった方も多いのではないでしょうか。
しかしソフトバンクでお得意の好評キャンペーン第2弾が開催されることになりました。
PayPay第2弾100億円キャンペーンが2019年2月12日(火)から開催されます。
第1弾はポイント還元が多すぎて、すぐに100億円が底をつきましたが、第2弾はポイント還元を抑えているので急がなくても大丈夫だと思われるので、PayPay残高へのポイント還元を最大限にもらえる準備をしっかりとしておきましょう。
今回は、PayPay第2弾100億円キャンペーンの概要とポイント還元を多くもらうための方法を解説したいと思います。
それでは早速見ていきましょう。
目次
PayPay第2弾100億円キャンペーンの概要

PayPayで実施される第2弾100億円キャンペーンの概要を解説します。
キャンペーン期間
2019年2月12日(火)から2019年5月31日(金)まで
ただし第1弾と同じで、キャンペーン期間中であってもポイント還元の付与金額が100億円に達した場合は、途中終了します。
キャンペーン特典
[st-midasibox title=”キャンペーン特典” fontawesome=”” bordercolor=”” color=”” bgcolor=”” borderwidth=”” borderradius=”” titleweight=”bold”]PayPay決済利用毎に利用金額の最大20%のPayPay残高を付与
[/st-midasibox]付与されるPayPay残高の付与率は支払い方法で変わります。
支払方法と付与率
PayPay残高またはYahoo!マネー=20%
Yahoo!JAPANカード=19%
その他のクレジットカード=10%

1回の支払いにおけPayPay残高付与の上限は最大1,000円相当でキャンペーン期間を通じての上限は5万円相当になります。
やたら当たるくじ
最大20%還元と同時に開催される「やたら当たるくじ」は当選すると、最大1,000円相当のPayPay残高が付与されます。
当選率
PayPayユーザー:10回に1回の確率で当選
Yahoo!プレミアム会員:5回に1回の確率で当選
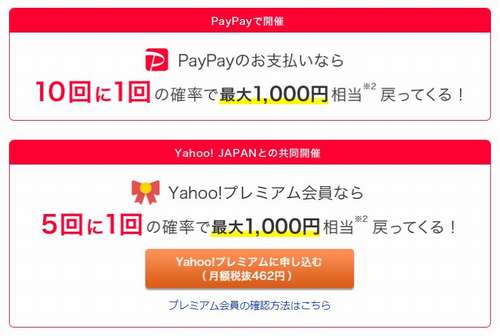
当選するのは、支払方法でPayPay残高、Yahoo!マネー、Yahoo!JAPANカードを利用した場合で、その他のクレジットカードを利用した場合は対象外になります。
やたら当たるくじのキャンペーン期間を通じてもらえる上限は2万円相当になります。
PayPay100億円あげちゃうキャンペーンとの違い

2018年12月に開催された100億円あげちゃうキャンペーンとの違いは次のことがあげられます。
PayPay残高の付与が最大50,000円相当から最大1,000円相当に
当選の全額還元で付与されるのが最大100,000円相当から最大1,000円相当に
支払方法でPayPay残高の付与率が変更
最大の違いは、付与されるPayPay残高の金額が最大5万円相当から最大1千円相当になったことですね。
第1弾では、PayPayユーザーが大挙して高額な商品を購入して大量の還元をもらったため100億円がすぐに底をつきましたが、第2弾は還元される金額が抑えられたので、長い期間利用できるのではないかと考えています。
PayPay残高の付与を最大限にもらう方法
PayPayの第2弾100億円キャンペーンは、PayPay残高の付与率や金額が変わったので、しっかりと準備をして最大限の還元がもらえるようにしましょう。
PayPayを利用する準備
PayPayの第2弾100億円キャンペーンを効率的に利用するためにおすすめする手続きは、次のとおりです。
[st-midasibox title=”おすすめの準備” fontawesome=”” bordercolor=”” color=”” bgcolor=”” borderwidth=”” borderradius=”” titleweight=”bold”]- Yahoo!プレミアム会員の登録
- Yahoo!JAPANカードの発行
- ジャパンネット銀行の口座開設
Yahoo!プレミアム会員は、月額税抜462円の会費が必要で、ソフトバンクユーザーは基本料金に含まれています。
ポイントサイトのモッピーを経由してYahoo!プレミアムの会員に申し込むと350円相当のポイントがもらえます。
第2弾100億円キャンペーンでは、Yahoo!プレミアム会員になると5回に1回の割合で1,000円まで全額還元されるので、キャンペーン期間中に登録してPayPayを利用してみてはいかがでしょうか。
ソフトバンクユーザーはYahoo!JAPANのIDと連携させてYahoo!プレミアムが使えるようにしておきましょう。
Yahoo!JAPANカードは、PayPay残高にチャージできる唯一のクレジットカードです。
本人認証が完了するとPayPayにチャージできるようになり、過去24時間で2万円まで、過去30日間で5万円までチャージできるようになります。
ジャパンネット銀行は、ヤフーが関連するネット銀行です。
PayPayとの相性が良く、チャージする銀行口座への登録が簡単にできます。
銀行口座からのチャージは、1日最大50万円まで、1月最大100万円までとなっています。
ジャパンネット銀行も、モッピーを経由して新規口座開設をすると1,100円相当のポイントがもらえます。

まだ、Yahoo!プレミアム会員の新規登録やジャパンネット銀行の新規口座開設をされていない方は、この機会にモッピーを経由して登録してみてください。
モッピーは、パソコン、スマホ、タブレットのどちらからでも登録できて、入会金、年会費もなく無料で使うことができますよ。
今ならモッピーの新規登録で最大1,300円相当のポイントがもらえるキャンペーンも実施しているので二重でお得になります。
第2弾100億円キャンペーンの利用方法
第2弾100億円キャンペーンで付与されるPayPay残高は最高で1,000円相当です。
PayPay残高で支払った場合、利用金額の20%が還元されるので、5,000円を利用すると1,000円相当のポイントが還元されることになります。
ただ、この場合「やたら当たるくじ」に当選しても、付与されるのは全額に当たる5,000円相当ではなく、1,000円相当ということで、キャンペーンで付与されるPayPay残高と同じです。
PayPayの利用金額を1,000円程度にしておけば、20%還元が確実にもらえて、くじに当選したときも最大1,000円相当の還元が丸々もらえます。
やたら当たるくじの当選も含めて考えると、1,000円程度の買物をするのが一番効率的ではないかと私は考えています。
まとめ
今回は、PayPay第2弾100億円キャンペーンの概要とポイント還元を多くもらうための方法を解説しましたが、いかがでしたか。
PayPayの第2弾100億円キャンペーンは、PayPay残高に付与される金額を抑えて、日常的に使えるキャンペーンになったのではないでしょうか。
ファミリーマートでPayPay残高を使って1,000円程度の買物をすると、キャンペーンの適用を受ける間は実質20%割引で買えることになりますし、やたら当たるくじに当選するとさらに還元率が上がります。
私も第1弾の「100億円あげちゃうキャンペーン」でPayPayを利用しましたが、使い方がすぐにわかってスムーズに支払いができました。
第2弾100億円キャンペーンも利用して損をすることがまったくないキャンペーンなので、まだPayPayを利用していない方は、アプリをダウンロードしてみてください。
モッピーに新規登録をしてから、モッピーのサイト内にある「Yahoo!プレミアム会員の新規登録」と「ジャパンネット銀行の新規口座開設」の広告を利用すると1,400円相当のポイントがもらえるので、こちらもぜひ利用してみてください。
あなたもモッピー経由で準備をして、PayPayの第2弾100億円キャンペーンを最大限の還元がもらえるようにしてみませんか。
今日も最後まで読んでいただいて、ありがとうございました。
このブログのランキングを上げるのにご協力いただける方は、下にある2つのボタンをそれぞれクリックしてください!
ため蔵に1票が入って、ブログランキングを見ることができます。



